Lingkaran 8 titik simetri

Nama : Putranto H N
Kelas : 2 DB 14
NPM : 31108529

Dalam geometri Euklid, sebuah lingkaran adalah himpunan semua titik pada bidang dalam jarak tertentu, yang disebut jari-jari, dari suatu titik tertentu, yang disebut pusat. Lingkaran adalah contoh dari kurva tertutup sederhana, membagi bidang menjadi bagian dalam dan bagian luar.

Unsur-unsur Lingkaran
Ada beberapa bagian lingkaran yang termasuk dalam unsur-unsur sebuah lingkaran. Di antaranya titik pusat, jari-jari, diameter, busur, tali busur, tembereng, juring dan apotema. Untuk lebih jelasnya, perhatikan uraian berikut.
A. Titik Pusat
Titik pusat lingkaran adalah titik yang terletak ditengah-tengah lingkaran. Titik 0 merupakan titik pusat lingkaran. Dengan demikian, lingkaran tersebut dinamakan lingkaran 0.
B. Jari-jari (r)
Jari-jari lingkaran adalah garis dari titik pusat lingkaran ke lengkungan lingkaran. Jari-jari lingkaran ditunjukkan oleh garis 0A, 0B dan 0C.
C. Diameter
Diameter adalah garis lurus yang menghubungkan dua titik pada lengkungan lingkaran dan melalui titik pusat.
D. Busur
Dalam lingkaran, busur merupakan garis lengkung yang terletak pada lengkungan lingkaran dan menghubungkan dua titk sembarang dilengkungan tersebut.
E. Tali Busur
Tali busur lingkaran adalah garis lurus dalam lingkaran yang menghubungkan dua titik pada lengkungan lingkaran. Berbeda dengan diameter, tali busur tidak melalui titik pusat lingkaran 0.
F. Tembereng
Tembereng adalah luas daerah dalam lingkaran yang dibatasi oleh busur dan tali busur.
G. Juring
Juring lingkaran adalah luas daerah dalam lingkaran yang dibatasi oleh dua buah jari-jarilingkaran dan busur yang diapit oleh kedua jari-jari lingkaran tersebut.
H. Apotema
Pada sebuah lingkaran, apotema merupakan garis yang menghubungkan titik pusat lingkaran dengan tali busur lingkaran tersebut. Garis yang dibentuk bersifat tegak lurus dengan tali busur.
Secara umum prosedur pembentuk lingkaran dibuat dengan rumus dasar x2+y2=R2. Terdapat beberapa cara untuk membentuk suatu lingkaran namun tidak efisien. Lingkaran dapat dibuat dengan menggambarkan seperempat lingkaran karena bagian lain dapat dibuat sebagai bagian yang simetris.

Lingkaran 8 titik
Lingkaran 8 titik pertama kali ditemukan oleh Louise Brand dari Cincinnati pada tahun 1944.



Algoritma Simetris delapan titik
Pada algoritma ini pembuatan lingkaran dilakukan dengan menentukan satu titik awal. Bila titik awal pada lingkaran(x,y) maka terdapat tiga posisi lain, sehingga dapat diperoleh delapan titik. Dengan demikian sebenarnya hanya diperlukan untuk menghitung segmen 45’ dalama menentukan lingkaran selengkapnya. Dengan titik pusat lingkaran tertentu, delapan titik simetris dapat ditampilkan dengan prosedur Circle Point Sebagai berikut:
procedure CirclePoints(x, y, value:integer);
begin
putPixel(x,y,value);
putPixel(-x,y,value);
putPixel(x,-y,value);
putPixel(-x,-y,value);
putPixel(y,x,value);
putPixel(-y,x,value);
putPixel(y,-x,value);
putPixel(-y,-x,value);
end;
Contoh Program Pascal :

Var X, Y, rad : integer;
procedure CirclePoints(x, y, value:integer);
procedure init;
var gd, gm : integer;
begin
gm:=detect;
gd:=0; InitGraph(gd,gm,'');
if GraphResult <> grOk then
begin
Writeln('Graph driver ',gd,' graph mode ',gm,' not supported');
Halt(1);
end;
end;
procedure destroy;
begin
closegraph;
end;
begin
writeln(‘Masukkan koordinat X : ‘);Readln(X);
writeln(‘Masukkan koordinat Y : ‘);Readln(Y);
writeln(‘Masukkan Radius : ‘);Readln(rad);
putPixel(X,Y,GetMaxX);
putPixel(-X,Y, GetMaxX);
putPixel(X,-Y, GetMaxX);
putPixel(-X,-Y, GetMaxX);
putPixel(Y,X, GetMaxX);
putPixel(-Y,X, GetMaxX);
putPixel(Y,-X, GetMaxX);
putPixel(-Y,-X, GetMaxX);
end;

Contoh Program
Uses graph;
Var
X, Y, rad : integer;
ErrorCode:integer;
GrDriver,GrMode:integer;
Begin
GrDriver:=Detect;
GrMode:=0;
InitGraph(GrDriver,GrMode,’ ‘);
ErrorCode := GraphResult; {Check for error}
If ErrorCode <> grOK then
Begin
Writeln(‘Graphics error :’);
Writeln(GraphErrorMsg(ErrorCode));
Writeln(‘Program Aborted…’);
Halt(1);
End;
ClearDevice; {do some graphics…}
Begin
Writeln(‘Masukkan Koordinat X : ‘);Readln(X);
Writeln(‘Masukkan Koordinat Y : ‘);Readln(Y);
Writeln(‘Tentukan Radius : ‘);Readln(rad);
PutPixel(X,Y,GetMaxX);
PutPixel(-X, Y,GetMaxX);
PutPixel(X, -Y,GetMaxX);
PutPixel(-X,-Y,GetMaxX);
PutPixel(Y,X,GetMaxX);
PutPixel(-Y,X,GetMaxX);
PutPixel(Y,-X,GetMaxX);
PutPixel(-Y,-X,GetMaxX);
Line(200,100,200,300);
Line(100,200,300,200);
Circle(200,200,rad);
Readln;
End;
CloseGraph;
End.

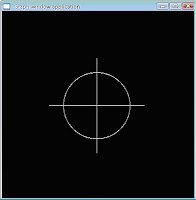
Hasilnya akan membentuk lingkaran seperti dibawah